GPU performance

I am currently doing a research paper for an English class titled; "Which GPU is Better for Scientific Computing; Nvidia GTX 480 or ATI HD5870?". I am amazed at the stats on the HD 5870. It has a raw computation rate for single point precision numbers rated at 2.72 teraflops per second. That is more than double the Nvidia card. The nvidia card, however, has a wider memory bandwidth which, as I described in my previous post, can severely affect performance, but the raw computational performance is simply amazing. I also read that the Nvidia card handles thread batching and memory latency more efficiently so maybe the real world performance difference isn't as grand. I have a HD5870 in a gaming system at home and I think i may take a look at some OpenCL programming in my spare time. Maybe I'll do a head to head with the GTX 280 in the lab.

Remember?

I remember saying that I was finished working on the matrix multiplication code. Well, I thought I was but after reading further into my text and watching some rather enlightening videos, I decided to write a new kernel. The reason I wrote a new kernel is because the first one had some flaws that were really slowing it down. The biggest flaw was my utilization of memory bandwidth and latency. The original code loaded the entire matrix into global memory. Global memory is the large but slow DRAM on the CUDA device. As a CUDA programmer I have access to a much faster, albeit much smaller, shared memory. The trick is to utilize the shared memory in such a way that I don't go over the 64KB limit(may be larger on the GTX 280). Turns out that there is a strategy for doing this.

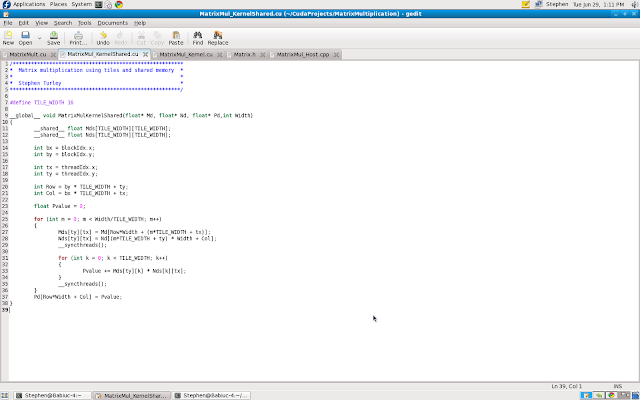
Let's look at the code:

You will notice at the top that I allocate two spaces in memory with the designation __shared__. This is how I tell CUDA that I want these variable stored in shared memory. You may be wondering why all the memory isn't shared if it is quicker. Well it is all about scope. The scope of global memory is device, meaning that every thread in the grid can access it at any time. When I store an entire matrix into the global memory and have thousands of threads accessing it, it creates quite a bottle neck. The scope of shared memory however, is block. This means that every thread in a block can access that blocks shared memory. It cannot, however, access another blocks shared memory. This keeps latency low and speed up. It also represents the physical layout of the memory cells on the chip.... but that is another story.

In order to stay withing the limiting size of shared memory I had to partition the matrix into what are called tiles. I made each tile 16X16 which is the same size of my blocks. Take a look at the code again and pay attention to the first for loop. Here each thread is responsible for loading an element into the shared sub-matrix. The following loop completes the calculation and the loop exits. The elements are then loaded back into global memory and the process is complete... well sort of.

The tricky part is realizing that we are executing 64 squared blocks of  16 squared threads. I have no way of controlling when the CUDA device will run each block, so I may have block 15,16 running first and block 1,65 running later and so on and so forth. Also one thread may take a little longer to execute than another. This is where the function __synchthreads(); comes in to play. This function is built into the metal so to speak. This just means that it is hardware instruction that tells all the threads in the block to wait until everybody is ready to move on to the next step. This is called a barrier synchronization.

Think of a barrier synchronization like kids getting on a bus. There may be 100 children running around screaming trying to find the correct bus to get them home. The children are like the threads... they know what they need to do but nobody knows when they will do it. So the bus driver must wait until everyone is on board before she departs. This is the barrier synchronization, the bus driver MUST wait for everyone. If she left early I'm sure there would be some very unhappy parents.

In the case of matrix multiplication, since every element must be loaded from the two input matrices for the threads to do their computations, I call __syncthreads() at the end of each element being loaded, and it makes the bus driver wait until the kids are on board.... or the threads are completed loading.

So all of this confusing tiling stuff must have done something. Check out this photo from the Nvidia CUDA visual profiler:

The bar graph illustrates clock cycles. The taller the bar, the longer it takes. Ignore the red and green bars and lets focus on the blue and yellow. The red and green are just memory moving around. The blue bar is my original kernel and the yellow is the new tiled/shared kernel. They do the exact same calculation but the shared kernel does it about 7 times faster! Pretty cool ehh?

Thanks for reading!

Quick update

It's been a while since my last post and I thought a short update was in order. I have been very busy this week, planning a vacation, working on a summer class, and learning CUDA. I spent two days in the lab and finished up my matrix multiplication code. I'm ready to start Monday on a new application that will do minimal and maximal array reductions. This is an important next step because it requires my kernel code to make logical decisions that will directly impact the efficiency of the algorithms. I have learned, and will explain in detail, that "for loops" and "if else statements" can dramatically increase computation time. Also I am learning the importance of using shared memory and the device registers to make code more efficient. Thankfully the CUDA SDK come with a very useful visual profiler that plots data showing how efficiently my code is running. I will have screen shots and full details this Tuesday so stay tuned!

Complexity Squared

  I have made some real progress climbing Mt. CUDA this week. I actually compiled and ran my first CUDA application.

  I decided to keep things simple by multiplying a pair of 2X2 matrices using a single block of 4 threads. One thread for each element of the product matrix. I could almost hear the CUDA device laugh as I wrote the code because this really isn't a very challenging problem for a CUDA solution. This is however a problem that can be solved using parallel methods so I thought, as do the books I'm reading, this was a good place to start. 

  Everything was pretty straight forward until I was ready to compile the code. For my first approach I just copied the build script that came with the CUDA SDK in an attempt to use it in my own code. It failed miserably and I soon found myself trying to learn how to write build scripts. Thankfully, I realized that this is really a pointless endeavor at this stage in the game because of the simplicity of the programs I am writing. This made me look at the nvcc compiler documentation and I learned that all I needed to do was write a simple command in the terminal and I could compile my code.

nvcc MatrixMult.cu -o MatrixMult

  I entered the above command and it worked! Here is a picture to prove it.

 Everything is working so I decided to make things a little more complex by multiplying a pair of randomly generated 256X256 matrices using a 4X4 grid of 4X4 blocks. This gives me 16 threads on 16 blocks for a grand total of 256 threads. This is a little bit more reasonable problem for CUDA but nowhere near the millions of threads that I have access to. 

  The added complexity of using more than one block of threads required me to do some extra math to derive the index of each element in the matrices. It is illustrated below:

//broken code

__global__ void MatrixMulKernel(int* Md, int* Nd, int* Pd, int Width)

{

//2D thread ID

int tx = threadIdx.x;

int ty = threadIdx.y;

int bx = blockIdx.x;

int by = blockIdx.y;

int row = (by * blockDim.y + ty);

int col = (bx * blockDim.x + tx);

//Pvalue stores the Pd element that is computed by the thread

int Pvalue = 0;

for (int k = 0; k < Width; k++)

{

Pvalue += Md[row * Width + k]* Nd[k * Width + col];

}

//Write the matrix to device memory each thread writes one element

Pd[row * Width + col] = Pvalue;

}

  You may notice that it says "//broken code" at the top of the code block. This is because this code is NOT working properly. I will show a screen shot of some output produced by this code and you may notice that only the products in the top left quadrant of the matrix "look" like reliable data. Keep in mind that my seed data are values from 0 to 4 for each element. I did this to keep the elements of the product matrix relatively small. I also shrunk the size of the matrix (after noticing a problem) to 32X32 in order to keep the complexity small. Now that only the top left quadrant "looks" like reliable data and the rest of the matrix has values far too small for them to be correct, this tells me a clue. I believe that only the block (0,0) is working correctly. I even checked some of the values by hand to prove this and found that some but not all values are correct. I checked element [0,0](correct) and [15,15](incorrect). This makes me think that I have an index derivation error in my code. Here is the screen shot... I will let my readers contemplate it as I do.

   So this is where I am. I am debugging some slightly more complex code. Hopefully it helps me discover new insights in this powerful technology. Thanks for reading!

*UPDATE*
 As I was proofreading my blog entry I think I have discovered the problem. With my current implementation of a 4X4 grid of 4X4 blocks the biggest matrix I can compute is 16X16 not 32X32 or 256X256! This is why only the 16X16 was computed in a manor that "looked" correct. The reason that the values were off in that block of the matrix is because I use the width of the matrix during the compilation and it was throwing everything off. I was falling off of the the thread array, so to speak. This is why it is important to take a step back, breathe, and look at everything from a fresh perspective. I was so worried about syntax and index derivation that I forgot to how to do some simple math. Garbage in garbage out, as they say. 

New banner!

A very special friend made me this shiny new banner shown above! I wonder if there is a message in it...?

I'm just having fun

It's been too long since I've posted on here. I could bore you with how busy I've been, but I think I will just tell you about some of the exciting things I've been learning. Also I am going to try to mix my blog posts with technical posts and posts aimed at the laymen. This post will be the latter. 

So due to the Memorial day holiday I was in the lab only one day this week. While there I split my time focusing on two topics. The main topic is CUDA, of course, and the other is the C/C++ programming languages. CUDA, as some of you may know, is written and developed using C/C++. This was the first language that I learned in high school but sadly I moved on to object oriented languages like Java and C#. So, I thought I should spend some time doing some review.

I found this great website that took me through two years of high school computer science in about two hours. I also installed Fedora 12 on my old laptop to practice developing on a similar platform at home.  It doesn't have a CUDA device installed but I can use it for C/C++ programming. 

Now what I'm really excited about. CUDA! I spent the rest of the day learning how to organize the multiple threads on the CUDA device. The more I read the more excited I became. This technology is the future, plain and simple. The power that CUDA gives a developer is really hard for me to imagine or visualize right now and I will tell you why.

It's all about threads! Think of a thread as stream of instructions that a compute device interprets. I use the word interpret very loosely here but that is beside the point. The point is that the old way of doing things is that a computer has one CPU that can handle one, two or maybe four threads. Thats it. A CUDA card can handle THOUSANDS, and it can handle all of those threads simultaneously. This is what I was talking about in my first post and is kind of old news. 

So what makes me so excited about it? Well, hold on and I will tell you. As you may imagine, dealing with thousands of anything can be pretty complicated and you probably shouldn't just "wing it". Thankfully the brilliant people over at Nvidia have came up with a very clever way of doing it. This is what excites me. The way that they do it. 

It goes something like this. When you are writing a program and you come to a point where lots of threads will be useful, you write a CUDA kernel. The kernel is what is executed by the threads. The kernel is just a set of instructions that is executed by a thread. Now we need to send this kernel off to a bunch of threads so it can be executed simultaneously. In-order to keep our data from getting lost in all of these threads, there must be a way for each thread to distinguish itself from the others. So when we invoke a kernel we send it off to what is called a grid. A grid is really just the grouping of threads that will execute this particular kernel. A grid has a structure which is 2 dimensional.  Within this 2D structure, or grid, there are 3D structures called "blocks". The blocks are where the threads live and you can use the location of the threads in the block and the blocks in the threads to give each thread a unique ID number. The ID is created using a little mathematical trickery which is pretty cool in its own right, but I won't go into that here. I will post a picture that I drew that lays it all out though. 

So in summary the threads are organized in a 3 dimensional structure, similar to a data structure called an array or matrix, and the locations within the structure are used to derive the unique identifier. I would like to call it a compute structure rather than a data structure but I'm probably just being silly. So thats what I've been up to!

Let's get parallel.

   I finally got to write some code today! Matrix multiplication is the "hello world" of parallel computation, so I figured that would be a good place to start. I think I should take this time to explain what matrix multiplication is and why it is a good function to port to a multi threaded platform like CUDA.  For simplicity I will be multiplying square matrices of equal size.
    First let me show an iterative implementation of matrix multiplication.
//C = A * B
//size is the width or height of the square matrix
for (int i = 0; i < size; i++)
{
  for (int j = 0; j
  {
      float sum = 0;
      for( int k = 0; k < size; k++)
     {
        float a = A[i * size + k]
        float b = B[k * size + j]
        sum += a * b;
     }
     C[i * size + j] = sum;
  }
}
Now for the CUDA implementation.
\
int tx = threadIdx.x;
int ty = threadIdx.y;

for (int k = 0; k < size; k++)
{
   float a = A[ty * size + k];
   float b = B[k * size + tx];
   float c += a * b;
}
C[ty * size + tx] = c;

 The first thing you will notice that the CUDA implementation is only one loop where the iterative implementation has three. The other thing you will notice is that there are two more variables int the CUDA code( tx and ty). They store the reference variables from threadIdx.x and threadIdx.y. This is how a CUDA thread distinguishes itself from the others. Since we use this index value to access the matrix, each thread will calculate the product of a single element of the product matrix C. The CUDA function is called a kernels, while the other is just a normal C function for the CPU or "host".

So this raises some more interesting questions. How does the compiler know what type of function you are writing and how are threads organized on a CUDA device?

CUDA introduces three new keywords to the C programming language; _device_, _global_, and _host_. These are used in the function declaration and tell the compiler what device will execute the code. _device_ is executed on the the CUDA device and called by the CUDA device. _global_ is executed on the CUDA device and called by the host, this is used to declare a kernel. All functions are defaulted as _host_ functions and are executed on the CPU and called by the CPU. If you don't use one of these keywords then the compiler treats it as a _host_ function. This makes code easier to port over to CUDA.

Soooooo what about these thread things? Well it goes like this... A grid is a two dimensional grouping of blocks.One grid per device (I think...).  Blocks are 3 dimensional groups of threads. You can have up to 512 threads per block and like 65,000 blocks per grid dimension. How you organize these is up to you.

You organize these blocks when you invoke a kernel. Here is the code for kernel invocation.

CudaFunctionName<<<dimGrid,dimBlock>>>("function parameters");

The new CUDA syntax is those "<<<,>>>" that you see above. This is how you pass the kernel configuration to the device. The two variables provide the dimensions of the grid and block. This is basically saying I want X number of blocks with Y number of threads for this kernel.

I've also been learning how to allocate and copy memory in CUDA and was going to explain that here. My post is getting a bit long so I think I will save that for next time. So until then I will leave you with this beautiful image of a Mandelbrot set I made using the CUDA SDK code examples.